This article is part of a series on performance guidelines.
Ask most programmers without previous GPU programming
experience how they’d go about writing a parallel sorting algorithm, and most
will tentatively forward the same approach: subdivide your unsorted list into
small chunks, and have each thread process them individually using a standard
linear sorting algorithm (usually quicksort – people love quicksort), somehow
magically merging the small sorted lists into our output list. This won’t work,
and to understand why we need to focus on how memory access and caching is
handled in a typical GPU.
Architecture
Like a CPU, the GPU memory model has Level 1 and 2 caches
(hence a need for locality) but a much heftier penalty for a cache miss. For
example, for a Fermi card, expect a few clock cycles for shared memory / L1
access and potentially hundreds of cycles for off-chip global memory access.

Usually the L1 cache is held within each SM (Streaming
Multiprocessor), while the L2 banks are shared. The memory interface is fairly
wide (for a Fermi card, for instance, its 384-bit wide, allowing for 12 contiguous
32-bit words to be fetch from memory at once per ½ clock cycle).
Finally, the PCI Express bus bridges access between the GPU
and the host memory, resulting in another layer of indirection and possible
bottleneck. Moving memory between host and device can be approximately one
order of magnitude slower than on-device memory access.
Shared memory
Besides L1 storage, the SM’s on-chip memory is also used as
shared memory, visible by all threads within a block. Shared memory’s usage
pattern is as a staging area for global memory load and storage; in other
words, instead of relying on the L1 cache’s algorithms to decide what to cache
and what to skip, the programmer uses shared memory to get precise control over
what gets stored in the L1 memory banks. Of course, the more memory we
explicitly allocate as shared memory, the less we have for L1, and vice-versa.
Bank conflicts

Shared memory is distributed across a number of equally-sized banks, usually as many as the warp size; contiguous elements in a shared memory buffer will be stored in contiguous banks. Since each bank can process only one memory access per clock cycle (multicasting as needed, serving several threads within a warp requesting the same index), if more than one thread in the warp accesses different indexes within the same block then a bank conflict happens, where each thread access is serialized, resulting in performance degradation. Simply put:
In a given clock cycle and for any threads A and B within
the same warp: if thread A accesses shared memory index X and thread B accesses
index X+U*32, for any X and any U!=0, then a bank conflict will happen.
Coalesced global memory access
We’ve already established just how costly global memory
access can be. But at times it just can’t be helped, for instance, when loading
global memory to a temporary storage buffer in shared memory used for further
computations.
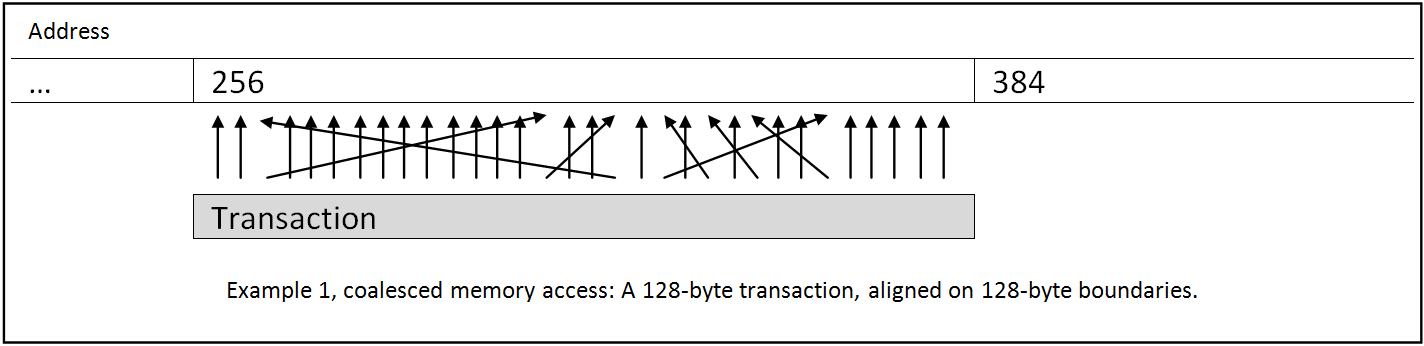
Each global memory access is packed into a contiguous 128
byte transaction (on recent architectures). Such transactions will read exactly
128 bytes from a 128 byte-aligned buffer in global memory. The transaction
itself is also aligned on 128 byte-boundaries.
Ideally each thread in a warp participates in the request,
specifying which part of a contiguous 128 bytes block in global memory it will
be accessing. In the end, all the threads in the warp will be serviced by a
single transaction (4 bytes * 32 threads = 128 bytes).
If each thread reads more than a 32-bit word, or if the
addresses requested extend beyond a 128 byte-aligned buffer, more transactions
need to be issued (with separate transactions for each separate 128-byte line
that is touched). The particular index within the 128-byte segment accessed by
each thread in a warp is no longer relevant for recent GPU architectures (but
for backward compatibility, the access should be sequential).

Because of these restrictions, it is often good practice
padding the end of data structures in order to preserve the 128-byte alignment.
For example, bidimensional arrays stored in a contiguous buffer may need extra
padding at the end of each row, ensuring that the next row begins at a 128-byte
boundary.
Memory access guidelines
Let’s now revisit our naïf parallel sorting algorithm:
picture thousands of threads, each pseudo-randomly accessing memory, oblivious
of what the other threads are doing. Given a large enough problem size,
practically all of those memory accesses will naturally result in cache misses,
and each of these individual accesses would waste 120 bytes on each
corresponding transaction. We can imagine the memory interface as a 384-bit wide
keyhole, beyond which all threads are piling up, idly waiting for their turn to
wastefully access memory. Our naïf sorting algorithm is in fact a linear
algorithm.
This applies not only to sorting algorithms, but to a vast
class of problems. Due to its serial nature, it turns out that
Memory access is possibly the greatest bottleneck of
parallel computing.
To work around the memory access limitation, we have to
design our algorithms so that
1. Every
thread within a block should work with the same small memory buffer, for as
long as possible, before discarding it. This buffer should reside in shared
memory, which uses the same fast memory as the L1 cache.
2. Global
memory accesses within a warp should be coalesced.
3. Shared
memory bank conflicts should be avoided.
4. All
the cache programming techniques discussed previously for CPUs (like blocking)
also apply for GPUs, and are even more relevant given GPU memory access’s central
stage.
5. Avoid
frequent host memory access. Move the data once onto the device, and keep it
there. If you must move it, do it simultaneously with another operation, such
as running a kernel on the GPU.
Warp divergence
Once the memory access problem has been satisfactorily
solved, another aspect to optimize is the divergence within a warp. All threads
within a warp usually march in lockstep, each processing exactly the same
instruction in the same clock cycle. When they don’t we have a divergence,
i.e., a situation where the warp’s threads are forced to run different
execution paths, usually as a consequence of an “if” or a “case”. The way the
SM handles such divergent paths is to serialize their execution, keeping every
unused thread within the warp idle and thereby wasting resources.
Imagine the following instruction being processed within a
warp:
if
(threadIx < 16)
myVar = 0;
else
myVar = 16;
Within a 32-thread warp, the flow of events is:
1 – All threads process the conditional instruction;
2 – The threads 0 to 15 will assign their register, while
the remaining threads will stay idle;
3 - The threads 0 to 15 will stay idle, while the remaining
threads will assign the register.
But we can eliminate the divergence altogether if instead we
write
myVar
= (threadIx & 0x10);
At the very least, one should try not to split warps by
conditional instructions. The following would be acceptable:
if
(threadIx < 32)
myOtherVar *= 2;
else
myOtherVar = 0;
Because warp #1 processes the product by 2, while all
remaining warps assign 0 to the register, there’s no need for warp divergences
and therefore no threads are idle within the block.
Register spillage
Each thread has a limited number of registers available to
execute a program’s logic (usually, up to 32 per thread, on a modern
architecture), which is a potential bottleneck. The compiler will try its best
to reuse the registers as much as possible, but for some more complex
algorithms it simply won’t do. Once more than 32 registers are needed, L1
memory storage will be hijacked to emulate additional registers, but with an
obvious performance impact. The worst happens when even the L1 isn’t enough to
accommodate our program’s requirements and the GPU is forced to use global
memory to hold register values. At this point the performance will degrade enormously,
which should be avoided at all costs, usually by reorganizing an algorithm’s
code through clever programming.
